Math 5610 - Computational Linear Algebra

---

Project maintained by BrandonFurman Hosted on GitHub Pages — Theme by mattgraham

The purpose of this page is to compare the speeds of Gaussian Elimination (SquareSystemSolver), Jacobi Iteration (jacobiSolver), and the Gauss-Seidel Algorithm (gaussSeidelSolver). In each case the algorithm is given a randomly generated diagonally dominant coefficient matrix. For the iterative methods a tolerance of 0.00001 is used. A graph of CPU time vs. matrix size is given below.

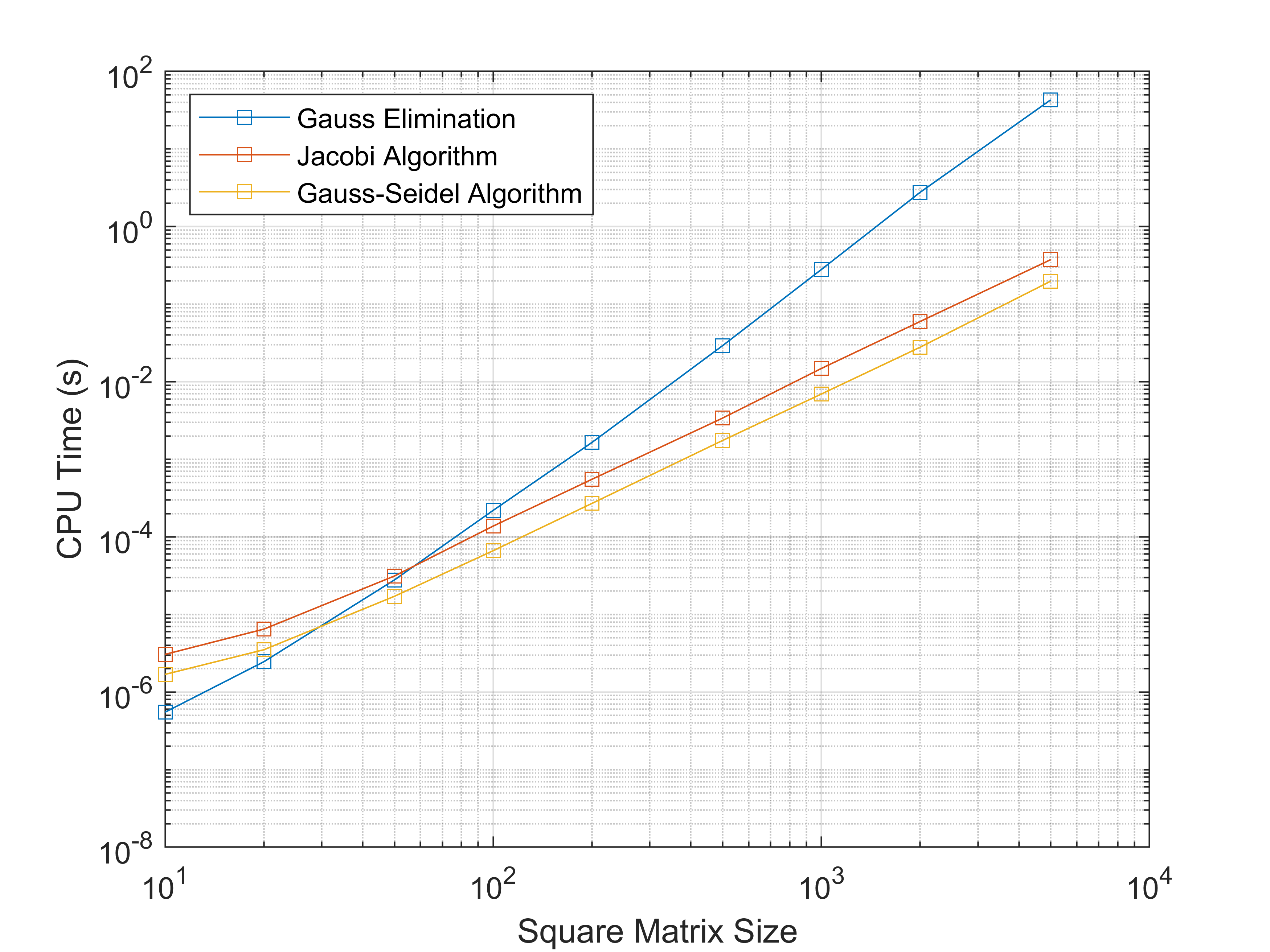
From this graph it can be seen that Gaussian Elimination is only faster for very small matrices. It can also be seen that the Gauss-Seidel Algorithm is consistently twice as fast as Jacobi Iteration.

int maxIter = 10000;
double tol = 0.00001;
int m = 5000;

array2D A;
array1D b, x, x1, x2, x3;

A = randDiagDomMat(m);
for (int i = 0; i < m; i++) A(i, i) += m;

b = randVec(m);
x = randVec(m);

std::clock_t time_req;

time_req = std::clock();
for (int i = 0; i < 100; i++) {
	x1 = gaussSeidelSolver(A, b, x, tol, maxIter);
}
time_req = clock() - time_req;


std::cout << "CPU time: "
	<< std::fixed << std::setprecision(10) << (double)time_req / (CLOCKS_PER_SEC*100.0) << " seconds" << std::endl;

	
time_req = std::clock();
for (int i = 0; i < 100000; i++) {
	x2 = SquareSystemSolver(A, b);
}
time_req = clock() - time_req;


std::cout << "CPU Time: "
	<< std::fixed << std::setprecision(10) << (double)time_req / (CLOCKS_PER_SEC*100000.0) << " seconds" << std::endl;