Math 5610 - Computational Linear Algebra

---

Project maintained by BrandonFurman Hosted on GitHub Pages — Theme by mattgraham

The purpose of this page is to compare the number of iterations it takes for the Jacobi algorithm and the Gauss-Seidel algorithm to converge. A diagonally dominant coefficient matrix is used. A tolerance of 0.0001 was used for both algorithms. The relevant data is shown below.

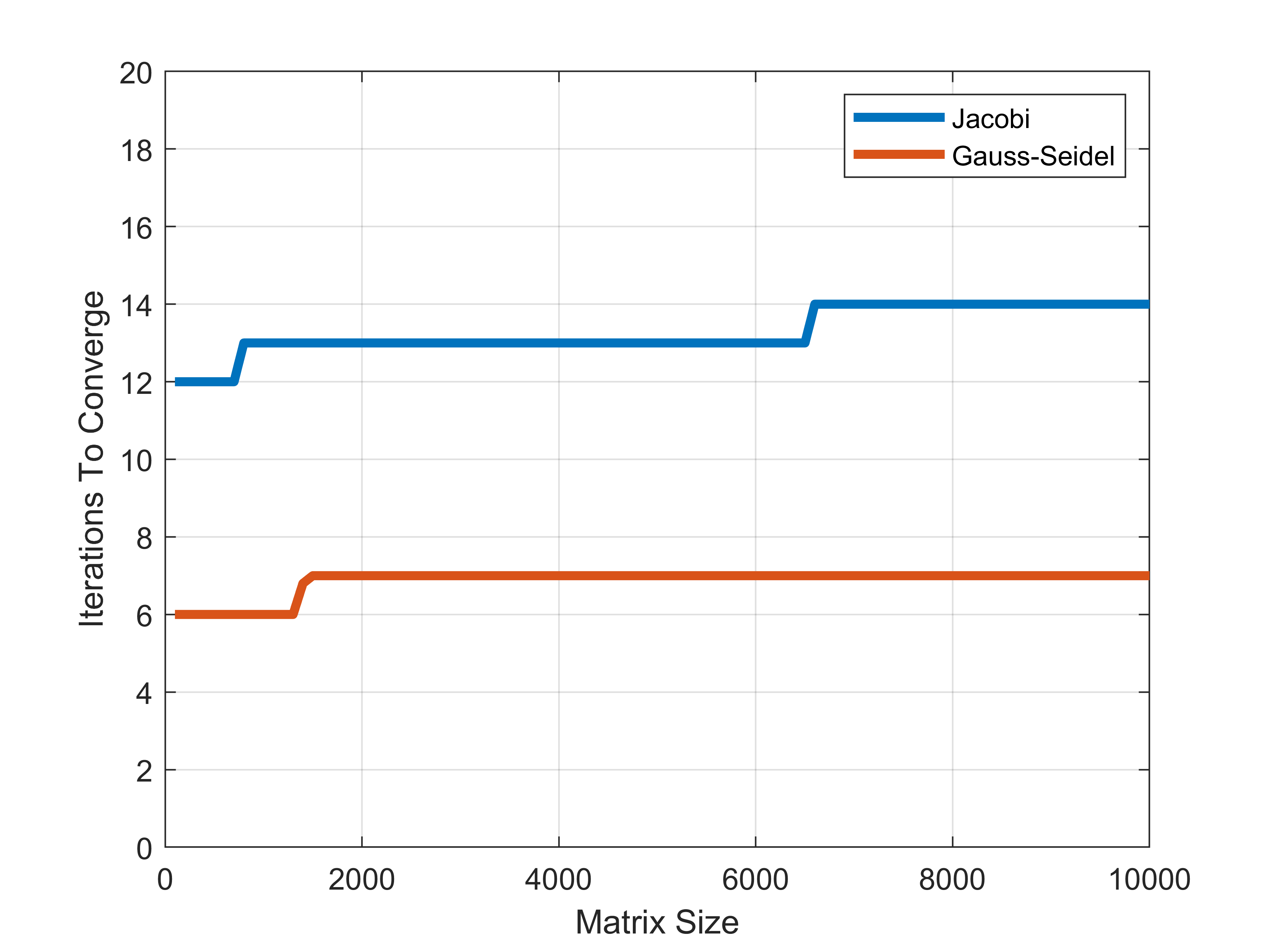
From this graph it can be seen that the Gauss-Seidel algorithm tends to converge twice as fast as the Jacobi algorithm. Additionally, the number of iterations it takes to converge tends to increase with increasing matrix size. This might be an artifact of how the diagonally dominant coefficient matrices were generated, however.